ANLDE system

ANLDE systems theory

Nonnegative Linear Diophantine Equations

Let $\mathbb{Z} = \{0, \pm 1, \pm 2, \ldots\}$ be a set of integers, $\mathbb{Z}_+ = \{0, 1, 2, \ldots\}$ be a set of nonnegative integers.

A system of nonnegative linear Diophantine equations (NLDE for short) is a linear system

$$Ax=b\,,\;\;\;\;\;\;\; A\in\mathbb{Z}^{n\times m}\,,\;\;\; b\in\mathbb{Z}^{n}\,,\;\;\; x\in\mathbb{Z}_+^{m}\,,$$ (1)

where $n$ is number of equations, $m$ is number of unknowns. Therefore, the solutions of a NLDE system are $m$-vectors with nonnegative integer components.

For example, consider the NLDE system with $n=2$ equations and $m=4$ unknowns:

$$\left\{\begin{array}{l} x_1 - x_2 + 3x_3 = 1 \\ x_1 + 2x_2 - x_4 = -1 \\ \end{array}\right.$$ (2)

This system has infinitely many solutions in  $\mathbb{Z}_+^4$. Among them, for instance, solutions $x=(0,2,1,5)^\top$ and $x'=(2,4,1,11)^\top$.

NLDE system (1) is homogenous, if $b$ is null vector $\mathbb{O}\in\mathbb{Z}^n$. Any homogenous NLDE system has the trivial solution $x=\mathbb{O}\in\mathbb{Z}_+^m$.

For any NLDE system a corresponding homogenous system can be constructed replacing right-hand side $b$ by $\mathbb{O}$. For example, the corresponding homogenous NLDE system for (2) is

$$\left\{\begin{array}{l} x_1 - x_2 + 3x_3 = 0 \\ x_1 + 2x_2 - x_4 = 0 \\ \end{array}\right.$$ (3)

If $x$ is a solution of (1) and $h$ is a solution of the corresponding homogeneous system, then $x' = x + \alpha h$ is also a solution of (1) for any nonnegative integer $\alpha$.

Nontrivial solution $h$ of homogenous NLDE system is indecomposable if it is not a sum of two nontrivial solutions of the same homogenous system. Solution $x$ of NLDE system (1) is indecomposable if it is not a sum of another solution $x'$ and a nontrivial solution $h$ of the corresponding homogenous system. For instance, the solution $x'=(2,4,1,11)^\top = (0,2,1,5)^\top + (2,2,0,6)^\top$ of NLDE system (2) is decomposable. The solution $h'=(2,2,0,6)^\top=(1,1,0,3)^\top+(1,1,0,3)^\top$ of the homogenous system (3) is decomposable. The solutions $x=(0,2,1,5)^\top$ and $h=(1,1,0,3)^\top$ (of NLDE systems (2) and (3) respectively) are indecomposable.

The notion ``a indecomposable solution'' for NLDE systems is equivalent to ``a minimal solution'', where the minimality is considered with respect to standard component-wise ordering. For example, $x=(0,2,1,5)^\top$ is minimal (for system (2)) and, therefore, there is no another solution $x'$ such that $x'\leq x$; $h=(1,1,0,3)^\top$ is minimal (for system (3)) and, therefore, there is no another (nontrivial) solution $h'$ such that $h'\leq h$

Hilbert basis of NLDE system (1) is a pair $(\mathcal{N},\mathcal{H})$, where $N\subset\mathbb{Z}_+^m$ is the set of all minimal (indecomposable) solutions of the NLDE system, and $\mathcal{H}$ is the set of all minimal (indecomposable) solutions of the corresponding homogenous system.

Sets $\mathcal{N}$ and $\mathcal{H}$ are always finite. They describe the set of all solutions of (1). Namely, any solution $x$ can be computed as:

$$x = x^{(l)} + \sum_{s=1}^q \alpha_s h^{(s)} \;\;\; \mbox{for some $x^{(l)}\in\mathcal{N}$\ and $\alpha_s\in\mathbb{Z}_+$} ,$$ (4)

where $p$ and $q$ are the numbers of solutions in the basis: $\mathcal{N}=\{ x^{(1)}, \ldots, x^{(p)}\}$, $\mathcal{H}=\{ h^{(1)}, \ldots, h^{(q)}\}$.

For example, all solutions of NLDE system (2) are described by the formula:

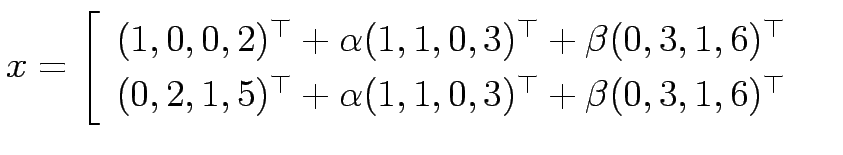$$x = \left[\begin{array}{l} (1,0,0,2)^\top + \alpha(1,1,0,3)^\top ... ...^\top + \alpha(1,1,0,3)^\top + \beta(0,3,1,6)^\top\\ \end{array}\right. \;\;\;$$ for $\forall\;\alpha, \beta \in \mathbb{Z}_+$$$, %$$$

where the left square bracket means alternation, ${p=q=2}$, ${\mathcal{N}=\left\{ x^{(1)}\!=\!(1,0,0,2)^\top, x^{(2)}\!=\!(0,2,1,5)^\top\right\}}$, ${\mathcal{H}=\left\{h^{(1)}\!=\!(1,1,0,3)^\top, h^{(2)}\!=\!(0,3,1,6)^\top\right\}}$. Taking $x^{(2)}=(0,2,1,5)^\top$, $\alpha=2$, $\beta=0$ we get the solution $x'=(2,4,1,11)^\top$.

This is very simular to the theory of linear equations: general solution is a sum of a particular solution and a linear combination of homogenous ones. However, the NLDE case has its own specifics: one particular solution is not enough to describe all solutions; there must be a set (but finite) of particular solutions. For the above example, at least two particular solutions are required.

See monograph [9] and papers [10,11] as classic introduction to the area.

Complexity problems for NLDE systems

The basic computation problems for a given NLDE system are listed below.

1. Is the NLDE system solvable in nonnegative integers? (for the homogeneous case, only nontrivial solvability is considered.)
2. Searching a particular solution of the NLDE system (if any). It may include searching any particular solution or any minimal solution or a particular solution satisfied to some other criteria.
3. Searching Hilbert basis of the NLDE system.

The list can be prolonged. For instance, an interesting problem is counting basis solutions.

The listed problems are very complex in the computational sense. The solvability and particular solution searching problems are NP-complete [9]. The problem of searching Hilbert basis is even more complex--overNP.

This is a reason for discovering particular classes of NLDE systems that have efficient (polynomial) algorithms for solving. We suggest (basing on the original work of M. Filgueiras and A.-P. Tomás [1]) an interesting approach for this--using formal grammars to establish such classes of NLDE systems.

A formal grammar is assigned to a NLDE system and solution searching is moved from set  $\mathbb{Z}_+^m$ to a set of derivations in the grammar--one searches a derivation instead of a NLDE solution (see Figure 2). The idea is the same as in operations calculus, where the problem of solving an integral-differential equation is reduced to solving an algebraic equation in complex numbers.

Figure 2: Association between NLDE and formal grammars: a general view

The methods and algorithms of the formal grammars theory have been very developed starting from 50th. Our approach turns out that they can be fruitfully used to construct really efficient algorithms for solving some particular classes of NLDE system. The efficiency means here that the algorithms are polynomial or pseudo-polynomial (comparing with the general NP-complete and overNP case with exponential complexity). The pseudo-polynomiality allows to select those problems (from the set of complex ones) that are permissible for practical solving.

NLDE systems, associated with CF-grammars. The syntactic algorithms

Consider a CF-grammar $G=(N,\varSigma,P,\cdot)$ and two strings $v$ and $w$. Let $G$ have $m$ rules ( $P=\{r_1, r_2, \ldots, r_m\}$), $n$ nonterminals ( $N=\{A_1,A_2,\ldots,A_n\}$), and $t$ terminals ( $\varSigma=\{a_1,a_2,\ldots,a_t\}$). Grammar rules $r_i$ has the form $A \to \alpha$, where $\alpha$ is a string in $(N\cup\varSigma)^*$. The start nonterminal symbol is not required.

One can construct an associated with the grammar NLDE system (ANLDE system for short) as follows:

$$\left\{\begin{array}{l} \displaystyle \sum\limits_{i\in I_k} x_i ... ..., \ldots, n+t \;\;\mbox{(i.e.~for each terminal $a_{k-n}$)}, \end{array}\right.$$ (5)

where $I_1 \cup \ldots \cup I_n = \{1,2,\ldots,m\}$ is a partition of {1,...,m}, $\gamma_{ki} \in \mathbb{Z_+}$, $b_k \in \mathbb{Z}$. Let us denote this system as $S(G;v,w)$.

The ANLDE system has $m$ unknowns (correspond to $m$ grammar rules), $n+t$ equations (correspond to $n+t$ grammar symbols). Each set $I_k$ contains indices $i$ such that rule $r_i$ has right-hand side with nonterminal $A_k$, i.e.  $A_k \to \alpha$. The coefficients $\gamma_{ki}$ is the number of occurrences of nonterminal $A_k$ ( $b_k=\mathrm{occ}(\alpha^{(i)},A_k)$, $1\leq k\leq n$) and terminal $a_{k-n}$ ( $b_k=\mathrm{occ}(\alpha^{(i)},a_{k-n})$, $n+1 \leq k\leq n+t$) in the right-hand side of the rule $r_i=A\to\alpha^{(i)}$. The coefficients $b_k$ is the difference between the number of occurancies of $A_k$ ( $b_k=\mathrm{occ}(w,A_k)-\mathrm{occ}(v,A_k)$, $1\leq k\leq n$) and $a_{k-n}$ ( $b_k=\mathrm{occ}(w,a_{k-n})-\mathrm{occ}(v,a_{k-n})$, $n+1 \leq k\leq n+t$) in the strings $w$ and $v$.

For example, consider the grammar $G_1$ with nonterminals $A$ and $B$ ($n=2$), the only terminal $a$ ($t=1$) and $m=4$ rules (listed in Table 1, col. 1).

Table 1: An example of ANLDE system

CF-grammar	ANLDE system (original)	ANLDE system (reduced)
$$\displaystyle \begin{array}{rl} r_1: & A \to AAB \\ r_2: & A... ...r_3: & B \to AAAaB \\ r_4: & B \to \varepsilon \\ \end{array}$$	$$\displaystyle \begin{array}{rl} A: & (x_1 + x_2) - (2x_1 + 3x... ... (x_1 + 2x_2 + x_3) = 1 \\ a: & 2x_2 + x_3 = 5 \\ \end{array}$$	$$\left\{\begin{array}{l} x_1 - x_2 + 3x_3 = 1 \\ x_1 + 2x_2 - x_4 = -1 \\ 2x_2 + x_3 = 5 \\ \end{array}\right.$$

$\varepsilon$ is empty string
Each grammar rule is marked with corresponding $r_i$
Each equation of the ANLDE system is market with a corresponding grammar symbol

Let $v=B$ and $w=aaAaaa$. Then the ANLDE system for the grammar $G_1$ has the form, presented in Table 1, col. 2. The simplified system is shown in col. 3.

Let us note the requirement $I_1 \cup \ldots \cup I_n = \{1,2,\ldots,m\}$ may be reduced to $I_1 \cup \ldots \cup I_n \subset \{1,2,\ldots,m\}$. If there is some $i\notin I_1 \cup \ldots \cup I_n$, then one can add $x_i$ to both sides of some equation (but exactly to one equation!). For example, the NLDE system

$$\left\{\begin{array}{l} (x_1 + x_2) - (2x_1 + 3x_3) = -1 \\ x_4 - (x_1 + 2x_2) = 1 \\ 2x_2 + x_3 = 5 \\ \end{array}\right.$$

is not in form (5), because $3 \notin I_1\cup I_2 = \{1,2\} \cup \{4\}$. Adding $x_3$ to the second equation we get the same ANLDE system as in Table 1

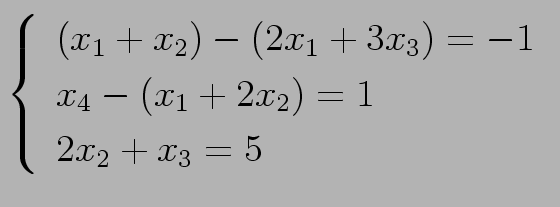
The following theorem shows the relation between derivations in a CF-grammar and solutions of the ANLDE system.

Theorem 1   Let $v \Rightarrow^* w$ be a derivation in CF-grammar $G$, $x_i$ is the number of applications of rule $r_i$ in this derivation (i=1,2,...,m). Then $x=(x_1,x_2,\ldots,x_m)$ is a solution of ANLDE system $S(G;v,w)$.

Therefore, for the ANLDE system form Table 1, each successful derivation $B \Rightarrow^* aaAaaa$ corresponds to a solution. Consider such a derivation:

$$B \stackrel{r_3}{\Longrightarrow} AAAaB \stackrel{r_4}{\Longright... ...rel{r_2}{\Longrightarrow} aaAaBBaa \stackrel{r_4,r_4}{\Longrightarrow} aaAaaa$$

Rule $r_1$ is not applied, so $x_1=0$; rule $r_2$ is applied two times, so $x_2=2$; rule $r_3$ is applied one time, $x_3=1$; rule $r_4$ is applied five times, $x_4=5$. Thus, we get a solution $x=(0,2,1,5)^\top$.

Definition of ANLDE system does not take into account the order of symbols in strings ($v$, $w$, right-hand sides of rules $r_i$). Let us define $\{\alpha\}^\circ$ as a multiset of all symbols of $\alpha$ (the number of occurances is taken into account!). For example, $\{abaaabA\}^\circ = \{A,a,a,a,a,b,b\} = \{A^1,a^4,b^2\}$. Using this notation, $\{\alpha\}^\circ = \{\beta\}^\circ$ means that the strings $\alpha$ and $\beta$ differ in order of symbols only. Binary operation $\triangle$ is a symmetric difference of two multisets.

Theorem 2   Let $G'$ and $G''$ are CF-grammars with the same alphabet  $N\cup\varSigma$; $v'$, $w'$, $v''$, $w''$ are strings in this alphabet. If $\{\alpha_i'\}^\circ = \{\alpha_i''\}^\circ$ $\forall i=1,2,\ldots,m$, where $\alpha_i$ is a right-hand side of rule $r_i$, and $\{v'\}^\circ \triangle \{v''\}^\circ = \{w'\}^\circ \triangle \{w''\}^\circ$. Then $S(G';v',w') = S(G'';v'',w'')$.

According to the theorem, one can take the grammar $G_1$ (see the above example) and $(v,w)=(BA,aaAaaaA)$. ANLDE system are the same. The derivation

$$BA \stackrel{r_3}{\Longrightarrow} AAAaBA \stackrel{r_4}{\Longrig... ...el{r_2}{\Longrightarrow} aaAaBBaaA \stackrel{r_4,r_4}{\Longrightarrow} aaAaaaA$$

constructs the mentioned above solution  $x=(0,2,1,5)^\top$. However, for $(v,w)=(B,aaaaaA)$ there is no derivation $B \Rightarrow^* aaaaaA$ in the grammar $G_1$.

This means one does not take into account i) the order of symbols in $r_i$, $v$, $w$ and ii) symmetric addition/subtraction of symbols in $v$, $w$.

Theorem 3   Vector  $x\in\mathbb{Z}_+^m$ is a solution of ANLDE system $S(G,v,w)$ if $x$ corresponds to a derivation $v' \Rightarrow^* w'$, where $\{v\}^\circ \triangle \{v'\}^\circ = \{w\}^\circ \triangle \{w'\}^\circ$ and the order of symbols in sentential forms is ignored.

ANLDE system format

The Web-SynDic system uses ANLDE systems in the following format:
# Comment
x1 + x2 + ... + xK2 = c11*x1 + c12*x2 + ... + c1N*xN
x[K2+1] + x[K2+2] + ... + xK3 = c21*x1 + c22*x2 + ... + c2N*xN
...
x[KM+1] + x[KM+2] + ... + xN = cM1*x1 + cM2*x2 + ... + cMN*xN

The format represents one ANLDE system. c11, c12, ..., c1N, c21, c22, ..., cMN are coefficients (optional, default value is 1). x1, x2, ..., xN are unknowns, may appear in any order, some may be skipped. If there is no unknowns after the ``='' sign, write ``0''. Each unknown must appear in the left-hand side of some equation at most one time. Blank and comment lines are ignored.

The sample of ANLDE system:
# Sample ANLDE system
x1 + x4 = 2*x1 + 3*x3
x2 + x3 = x1 + 2*x2 + x3

Format for a set of ANLDE systems is following:
<ANLDE system 1>
%
<ANLDE system 2>
%
...
<ANLDE System N>

The format represents ANLDE System Set <ANLDE System 1>, ..., <ANLDE System N>. Each system is in the ANLDE system format. Blank and comment lines are ignored. String with symbols(s) '%' is a delimiter for ANLDE systems. These strings may additionally contain blank symbols (' ', '\t') only.